 Linear programming involves finding optimal solutions to problems subject to linear equality
constraints.
Linear programming involves finding optimal solutions to problems subject to linear equality
constraints.
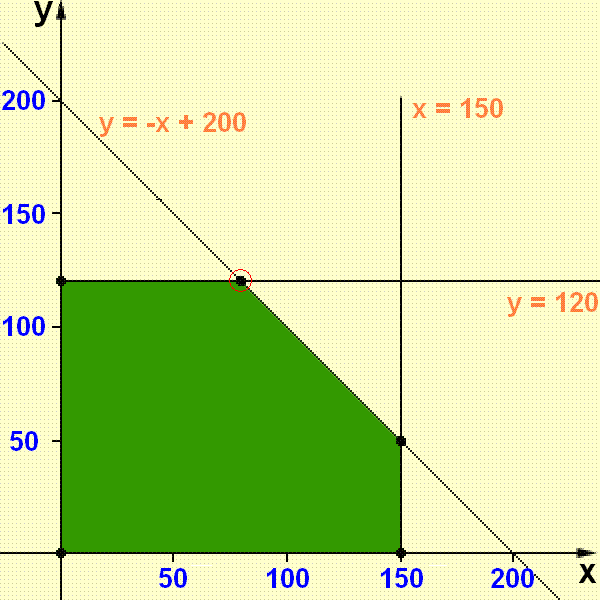
For example, a company can make 150 nuts and 120 bolts, but there is only material for making 200 items.
Each nut yields a profit of $2 and each bolt yields $5.
To maximize its profit (P), the constraints of the problem can be expressed as
The vertex that yields the maximum P is (x=80, y=120).
The maximum P is 2(80) + 5(120), or $760.